Georgia Tech OMSCS Graduate Algorithms Review | CS 6515

What is Graduate Algorithms?

Algorithms is the study of getting computers to do things fast and efficiently 🏃🏻‍♂️🚀

Graded Course Material

• 8 Homeworks (~%2 each)
• 3 Coding Project (%3 each)
• 3 Exams (%24 each)

Homework 0: Big-O Notation, Graph Theory and Boolean Logic

This is a self-assessment in how well you know:

• Big-O Notation
• Graph theory
• Boolean logic

Homework 1: Dynamic Programming

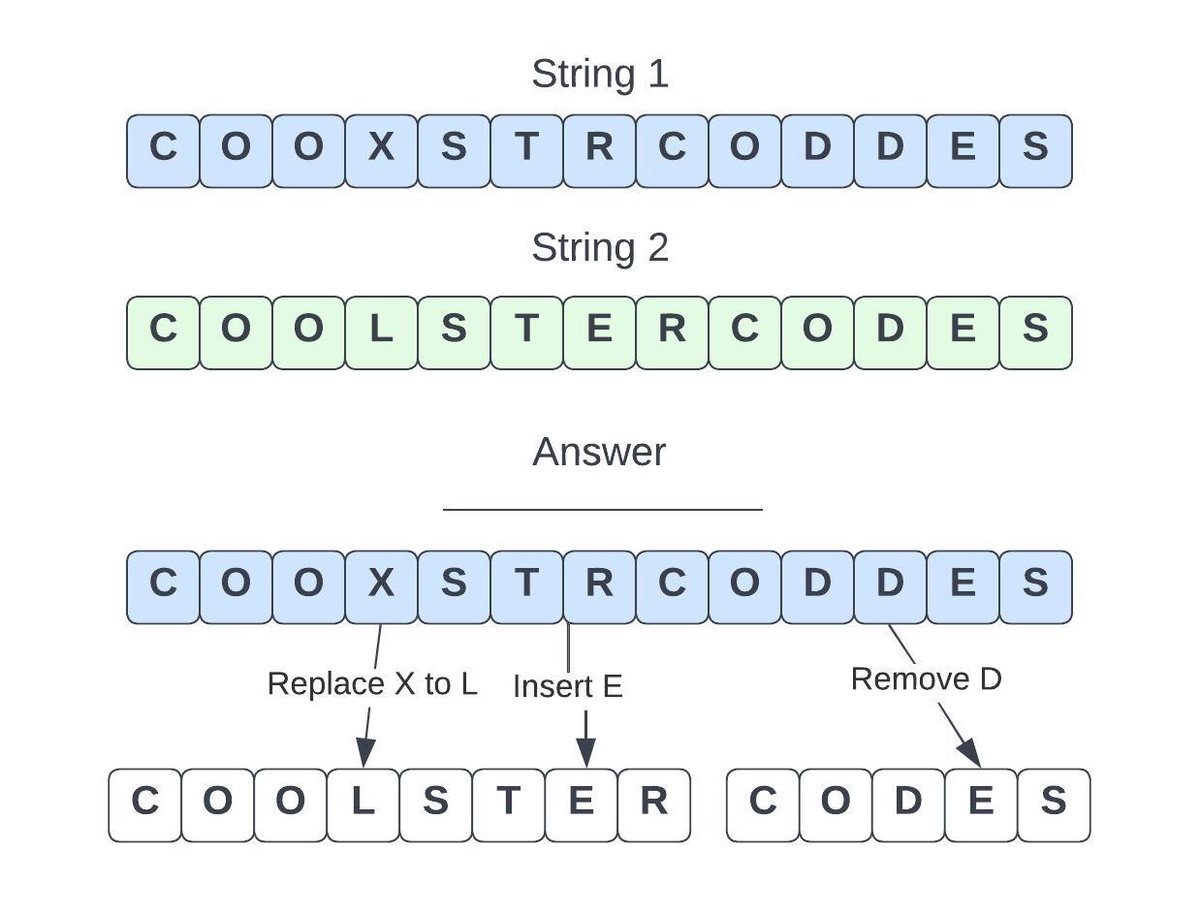
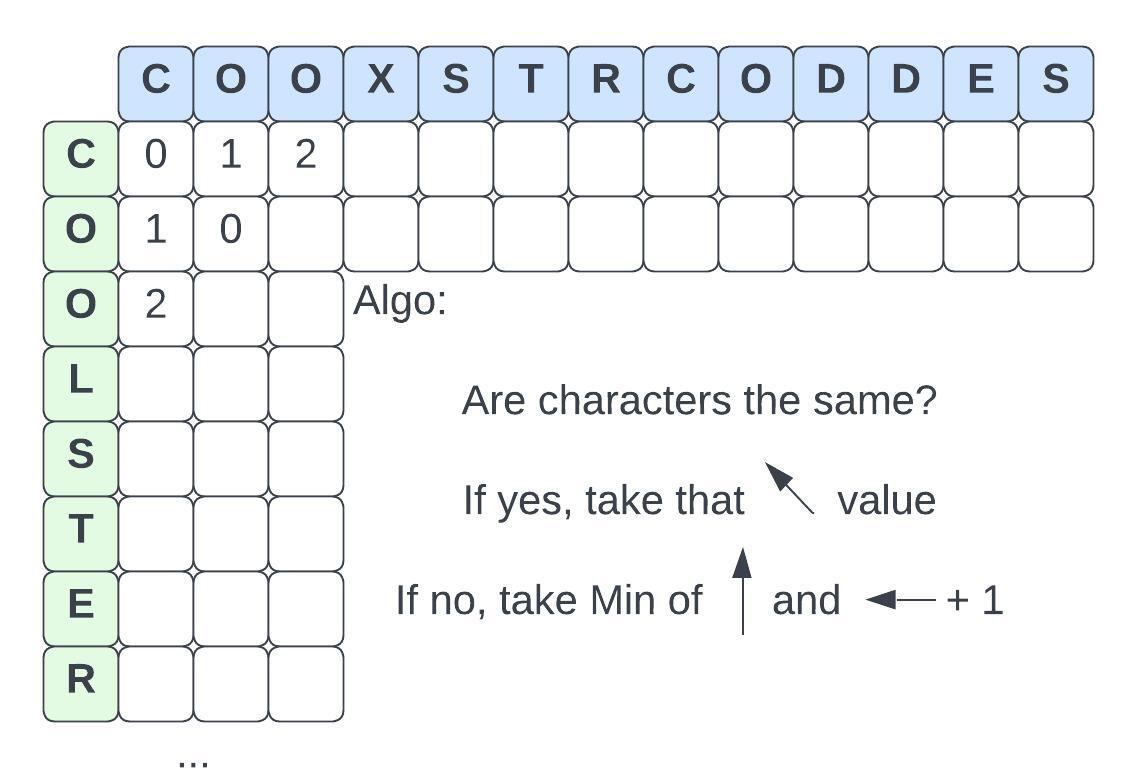
Example: Edit Distance

• You're trying to find out how “close” two words are
• The allowed actions are Replace, Insert and Remove

You can solve this using Dynamic Programming

Homework 2: Graphs and logarithmic

Example: Traveling Salesman Problem

• Try to find the shortest path between cities
• Actually super complicated 😱

Homework 3: Fast-Fourier Transform

• Fast Fourier Transform lets you break apart into pieces things like sound, electric signals etc.
• Sounds like it is super useful for stuff..
• I guess that's how Shazam works.. 🤷🏻‍♂️

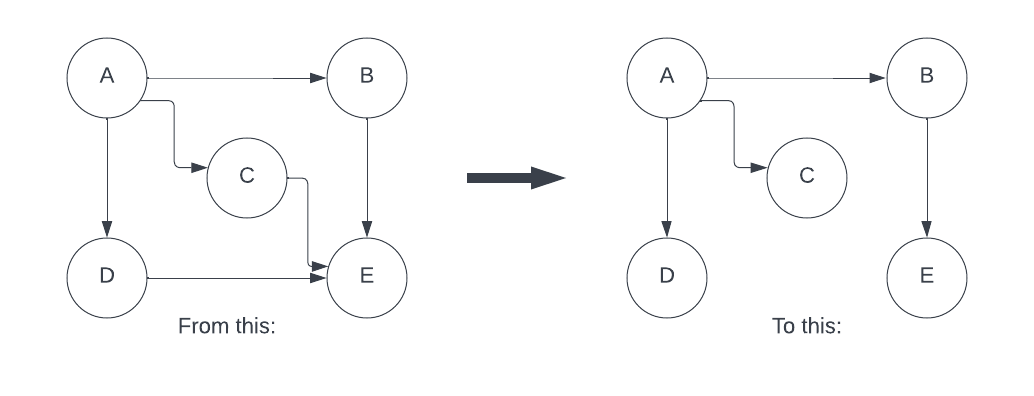
Homework 5: Minimum Spanning Trees

This one is about merging two MSTs together, using an algorithm that is efficient and correct

Homework 6: Modular math and RSA

RSA) is an encryption algorithm. It is how many things are “encrypted” these days - Basically, it comes down to the fact that it's really hard to find out the two prime numbers that make up a really big number

Project 1: Dynamic Programming

Dynamic programming is a way to break up a problem into a bunch of smaller problems that “add back up” to the original problem

Take for example, the Fibonacci sequence

• What is the nth Fibonacci number?

Recursive (slow) way:

def fib(n):
    if n <= 1:
        return n
    return fib(n-1) + fib(n-2)

Dymanic Programming! (fast way!)

def fib(n):
    a = 0
    b = 1
    if n == 0:
        return a
    elif n == 1:
        return b
    else:
        for i in range(2, n+1):
            c = a + b
            a = b
            b = c
        return b

In this project, you're solving the Knapsack Problem

Project 2: Minmum Spanning Tree w/ Kruskal's Algorithm

Minimum Spanning trees are basically just finding the most direct route from nodes in a graph.

In this project, you'll use Kruskal's algorithm to find the MST

You'll have to compute two things:

• Find(p): given the set p, find the root node of the set of nodes
• Union(u,v): given two sets of nodes, union them into an MST

Exams

• 2 Free response questions
• A prompt, followed by your input for an algorithm that satisfies the prompt

🚨 OPINION TIME! 🚨

• The content in this class is awesome
• I think this class relies too much on psuedo code
• Some more real code in this class would be great

Should you take this class?

If you are doing your master's for personal benefit, and just to learn something new, you may like this class's lecture videos

If you are doing your master's to perform well in academia, and kind of like that style of thing, maybe this is the class for you

If you are doing your master's to get your degree, I would suggest taking the Interactive Intelligence route and skipping this class