How Euclid Solved Programming 3,000 Years Ago

Greatest Common Divisor

Euclid in about 300 B.C. devised an algorithm for finding the greatest common divisor of two whole numbers

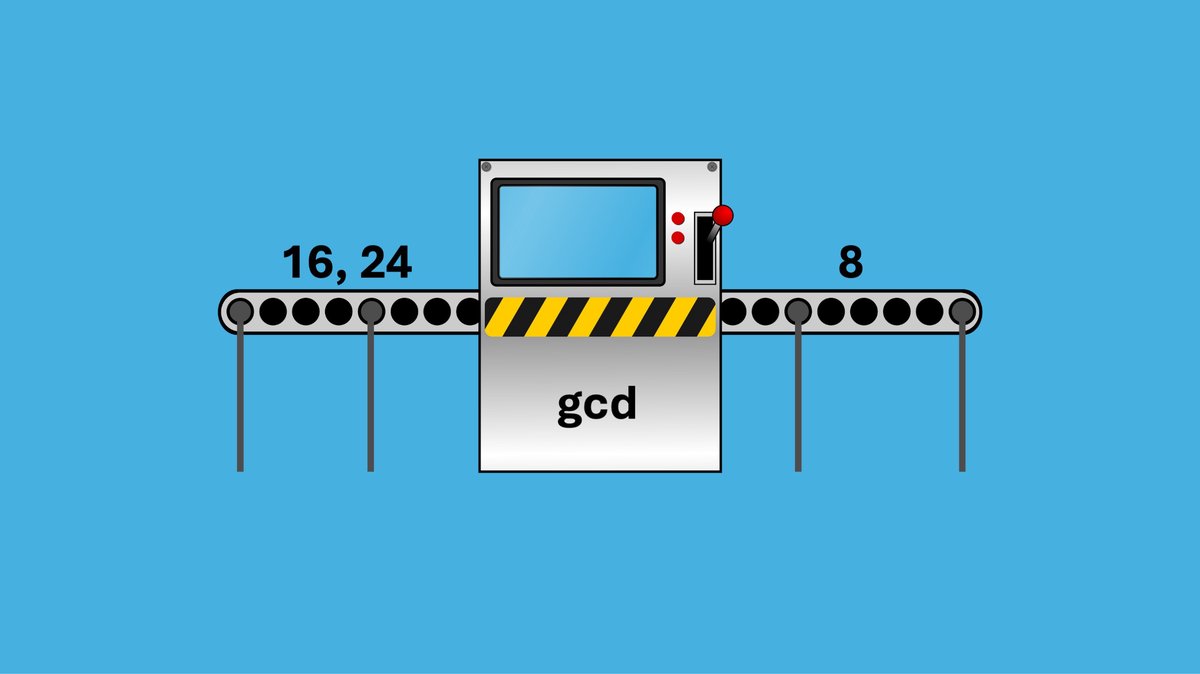
The slow way

One way to find the GCD of two numbers is to list out all the factors of each number, and iterate through each list to find the highest common number

The fast way

Let’s break this down:

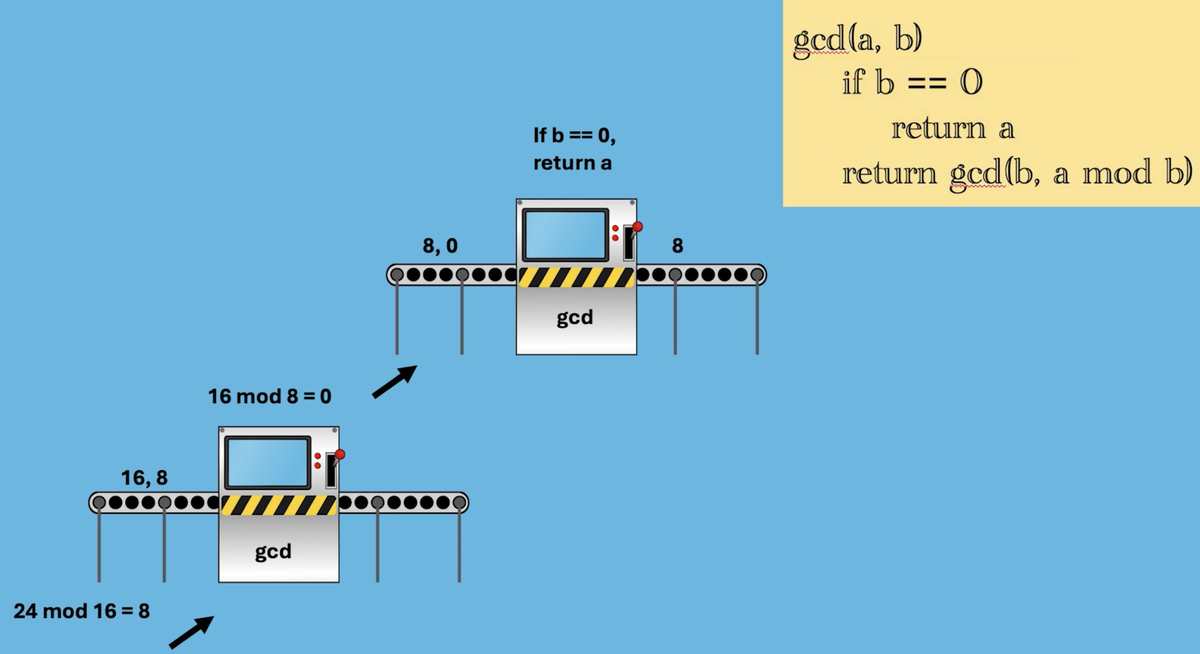
• gcd() symbolizes a “function call”
• The “function” is itself
• This is call Recursion

GCD broken down

This is where Modular Arithmetic is useful

Euclid’s algorithm calls for swapping a for b in the function call (i.e. the “recursive” call), and having the second argument be:

• a mod b

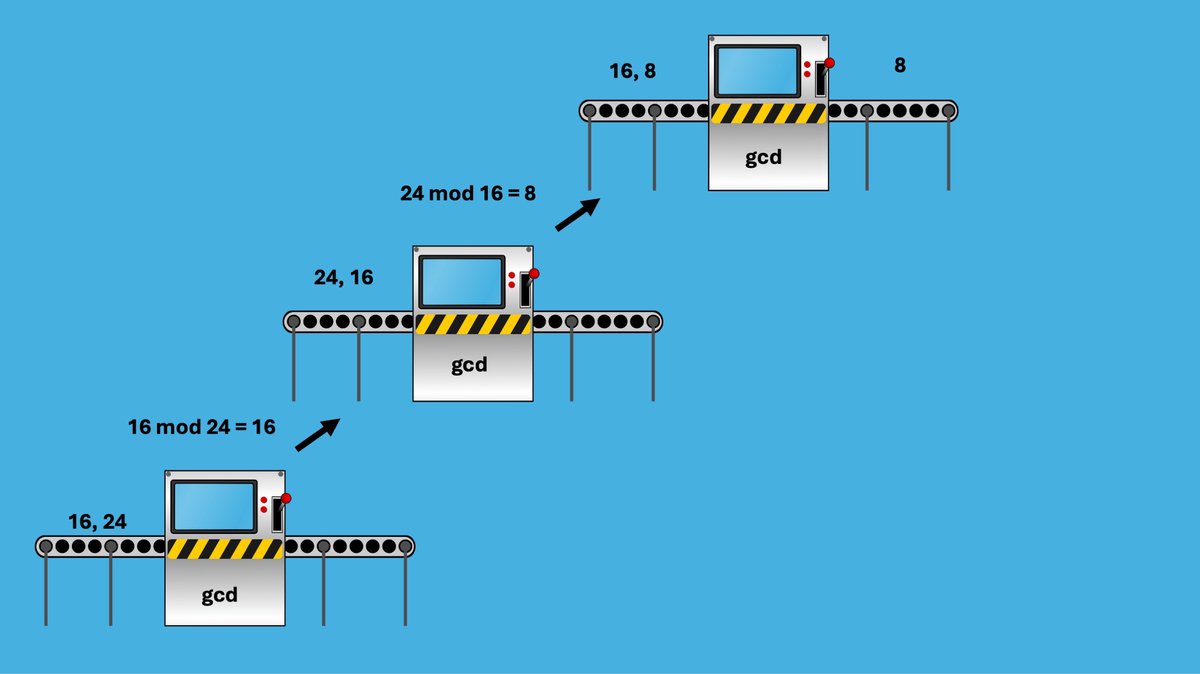
This means, that if a were 16 and b were 24, then 16 mod 24 is just 16, because 24 is bigger than 16, so 24 can’t divide 16 at all, so the remainder is just 16

On the next call however, 24 is modularly divisible by 16 (it leaves us with 8 left over)

So the next function call paramters are 16 and 8

The crazy thing about this algorithm

This still remains one of the FASTEST ways to get the GCD of two numbers

Even with all our fancy computing power, Euclid had this solved roughly 2-3,000 years ago 😂

What a baller 😎